


Next: Square roots of integers
Up: Modular mappings
Previous: Arbitrary powers
Working with complex numbers reduces to being able to compute
the signature of i, the imaginary unit.
Sn(i) should satisfy the basic relation of
Sn(i)2+1=0.
This means that
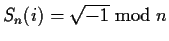 .
If n = 4k+1 is a prime, then -1is a non-residue, and we can find its square root.
If
n=n1 n2 ... is composite, then -1 should be a non-residue
for all ni.
As a consequence n has two possible forms, n=4k+1 or
n=8k+2.
Once that we have chosen n so that Sn(i) has a representation,
we still have two choices (plus and minus).
Any choice works provided that we use it consistently.
This choice is not yet a problem, but will become one
once that we introduce algebraic numbers in general.
This will be discussed later.
.
If n = 4k+1 is a prime, then -1is a non-residue, and we can find its square root.
If
n=n1 n2 ... is composite, then -1 should be a non-residue
for all ni.
As a consequence n has two possible forms, n=4k+1 or
n=8k+2.
Once that we have chosen n so that Sn(i) has a representation,
we still have two choices (plus and minus).
Any choice works provided that we use it consistently.
This choice is not yet a problem, but will become one
once that we introduce algebraic numbers in general.
This will be discussed later.
Suppose we want to test whether
(x+i)(x-i)-x2-1 is identically 0.
We can work with n=13, where S(i)=5 is a possible choice.
Selecting S(x)=2 as before we obtain
When we are forced to compute signatures in a field or congruence
which does not allow the representation of i, we will use field
extensions.
This will be described for the signatures of ex and
trigonometric functions.



Next: Square roots of integers
Up: Modular mappings
Previous: Arbitrary powers
Gaston Gonnet
1999-07-04