


Next: Estimating Mutation Matrices
Up: Better Dayhoff Matrices
Previous: The CreateDayMatrix Function
Recall, a 1-PAM mutation matrix measures a unit of evolution where the
expected change is exactly  of the amino acids.
It is clear that a 2-PAM evolution will not produce a 2%
change since some changes
may mutate back to the original amino acid. (A 2-PAM evolution is
equivalent to two separate 1-PAM evolutionary units.)
The percentage identity, pi, is defined to be the number of identical
bases between two sequences in an alignment. It is is related to the
PAM distance, p, by
of the amino acids.
It is clear that a 2-PAM evolution will not produce a 2%
change since some changes
may mutate back to the original amino acid. (A 2-PAM evolution is
equivalent to two separate 1-PAM evolutionary units.)
The percentage identity, pi, is defined to be the number of identical
bases between two sequences in an alignment. It is is related to the
PAM distance, p, by
In the above formula we need both the mutation matrix and the
frequency vector. The frequency vector can be derived
from any mutation matrix.
Recall the symmetry relation:
fi Mji = fj Mij
Setting j=1 and rearranging
On the other hand we know that
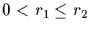 ,
consequently
,
consequently
The formula for pi(p) can be made independent of the frequencies
fi as:
for any mutation matrix M, in particular for Mp which
is also a mutation matrix.
The following function computes the percent identity for a
given PAM distance.
> PamToPerIdent := proc( pam:real, logPAM1:array(real,20,20) )
> description
> 'compute the percentage identity that a pam distance will leave';
> if pam < 0 then error('invalid percentage range') fi;
>
> num := den := 0;
> M := exp(pam*logPAM1);
> for i to 20 do
> num := num + M[i,1]*M[i,i]/M[1,i];
> den := den + M[i,1]/M[1,i]
> od;
> 100*num/den;
> end:
By definition, the following should be 99%
> PamToPerIdent(1,logPAM1);
99.0000
> PamToPerIdent(250,logPAM1);
16.9051
the classical PAM value gives about 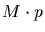 identity. Many believe
that approximately
identity. Many believe
that approximately 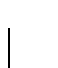 identity is needed to detect homology based
on sequence data alone.
identity is needed to detect homology based
on sequence data alone.
Computing the inverse function, PerIdentToPam, is somewhat more
difficult.
Since it is very unlikely that a closed form solution
exists, we use Newton's method for solving equations.
Newton's method begins with an initial guess x0 and computes x1,
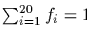 using
using
where g(x) is the equation to be solved in the
unknown x and gx'(x) is the derivative of
g(x) with respect to x.
In our case, the equation is
and our unknown is p, the PAM distance.
Computing the derivative of Mp with respect to pis not so complicated. Recall that M is a square matrix so
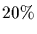 is also a square matrix and
using the series definition we can compute
is also a square matrix and
using the series definition we can compute
(M and 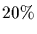 necessarily commute
under matrix multiplication).
As expected the derivative of powers of matrices
has the same expression as for scalars.
necessarily commute
under matrix multiplication).
As expected the derivative of powers of matrices
has the same expression as for scalars.
Consequently the derivative of the equation is
This exercise also shows how to protect a Newton iteration
from going astray by using binary search
techniques.
Newton's method may or may not converge on a solution. When it does,
it does so quickly. However, often it does not converge at all.
> PerIdentToPam := proc( pi:real, logPAM1:array(real,20,20) )
> description 'compute the PAM distance which results in the given
> percentage identity';
check the argument range and trivial case
> if pi <= 0 or pi > 100 then error('invalid percentage range') fi;
> if pi=100 then return(0) fi;
Compute the amino acid frequencies as described before
> AF := CreateArray(1..20);
> M := exp(logPAM1);
> for i to 20 do AF[i] := M[i,1]/M[1,i] od;
> AF := AF/sum(AF);
Now check that the percentage identity is not less than
its asymptotic value.
That is, for PAM
 ,
the percentage identity
does not decrease to zero but to the percentage identity
of two random sequences.
This value is
,
the percentage identity
does not decrease to zero but to the percentage identity
of two random sequences.
This value is
> asy := AF*AF;
> if pi/100 <= asy then
> error('pi cannot be less than the asymptotic value',100*asy) fi;
>
For reasons which escape the scope of this tutorial,
the following is a good initial guess
for the PAM value.
> pam := -100*ln(pi/100-asy);
Next, the PAM value will be bound below by lo
and above by hi. Setting the above bound to
5 times the initial guess is sufficient.
> lo := 0; hi := 5*pam;
We will now iterate until we reach the desired accuracy,
i.e. the difference between the bounds is close to
the machine epsilon.
> while hi-lo > hi*DBL_EPSILON*10 do
> mp := exp(pam*logPAM1);
> m1p := logPAM1*mp;
> num := -pi/100;
> den := 0;
> for i to 20 do
> num := num + AF[i]*mp[i,i];
> den := den + AF[i]*m1p[i,i]
> od;
Reset lo or hi as appropriate
> if num >= 0 then lo := pam else hi := pam fi;
> incr := -num/den;
> pam := pam + incr;
If the increment squared is relatively less than the
machine epsilon we can stop the iteration.
Notice that when doing Newton's iteration,
the relative error
is proportional to the square
of the previous relative error.
> if abs(incr)^2 < abs(pam)*DBL_EPSILON then break fi;
If the value falls outside the bounds, then
the Newton's value is not converging, so we just
compute the midpoint of the bounds as the next
guess.
> if pam <= lo or pam >= hi then pam := (lo+hi)/2 fi;
> od;
> pam
> end:
Again, by definition, the following should evaluate to 1.
> PerIdentToPam(99,logPAM1);
1.0000
A 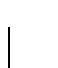 identity corresponds to PAM 278.5236.
identity corresponds to PAM 278.5236.
> PerIdentToPam(15,logPAM1);
278.5236



Next: Estimating Mutation Matrices
Up: Better Dayhoff Matrices
Previous: The CreateDayMatrix Function
Gaston Gonnet
1998-09-15
 of the amino acids.
It is clear that a 2-PAM evolution will not produce a 2%
change since some changes
may mutate back to the original amino acid. (A 2-PAM evolution is
equivalent to two separate 1-PAM evolutionary units.)
The percentage identity, pi, is defined to be the number of identical
bases between two sequences in an alignment. It is is related to the
PAM distance, p, by
of the amino acids.
It is clear that a 2-PAM evolution will not produce a 2%
change since some changes
may mutate back to the original amino acid. (A 2-PAM evolution is
equivalent to two separate 1-PAM evolutionary units.)
The percentage identity, pi, is defined to be the number of identical
bases between two sequences in an alignment. It is is related to the
PAM distance, p, by
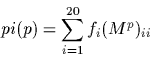
 identity is needed to detect homology based
on sequence data alone.
identity is needed to detect homology based
on sequence data alone.
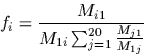

 ,
the percentage identity
does not decrease to zero but to the percentage identity
of two random sequences.
This value is
,
the percentage identity
does not decrease to zero but to the percentage identity
of two random sequences.
This value is
 identity corresponds to PAM 278.5236.
identity corresponds to PAM 278.5236.