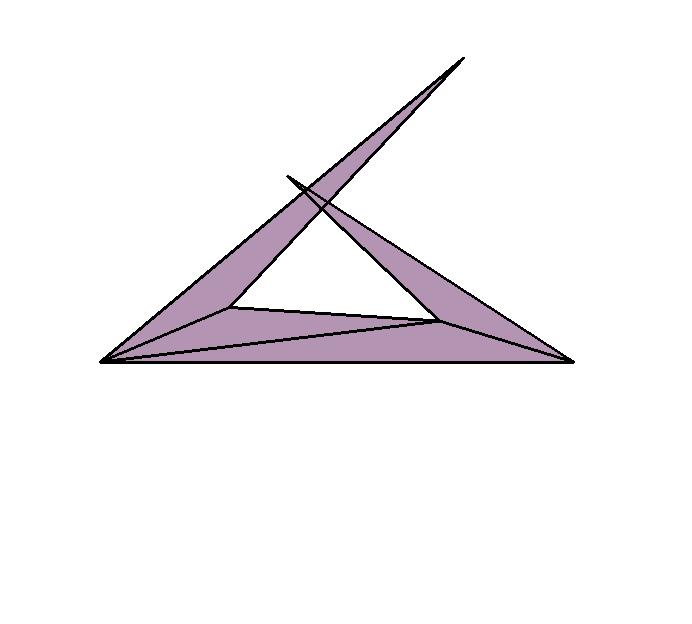
Fig. 1. Selfoverlapping unfolding by Namiki (Click here for ps file).
An unfolding of a convex polytope P in R^3 is a planar embedding of its boundary obtained by cutting the edges of some spanning tree T of the graph of P and flattening the boundary along the remaining edges. Two natural (but naive) questions are
Here an unfolding is defined to be unambiguous if the original polytope is uniquely constructible from it.
Both questions have negative answers. There are many constructions known for the negative answer of (a), but Makoto Namiki (namiki@waka.c.u-tokyo.ac.jp) constructed the smallest example, a skinny tetrahedron, which admits a selfoverlapping unfolding:

Fig. 1. Selfoverlapping unfolding by Namiki (Click
here for ps file).
Note that it has a non-selfoverlapping unfolding as well. For the question (b), Tomomi Matsui (tomomi@misojiro.t.u-tokyo.ac.jp) constructed a polytope with 6 facets and 5 vertices which admits an ambiguous unfolding:

Fig. 2. Geometrically ambiguous unfolding by Matsui (Click
here for ps file).
These two examples can be found in the UnfoldPolytope package for Mathematica by Namiki and Fukuda [NF92].
Consequently more intelligent questions are
As far as I know, these questions are still open. I conjectured at the Dagstuhl meeting on Computational Geometry (February 1997) that
The positive answer to this would resolve the question (a') positively as well.
Recently Günter Rote (rote@opt.math.tu-graz.ac.at) has constructed counterexamples to this conjecture:
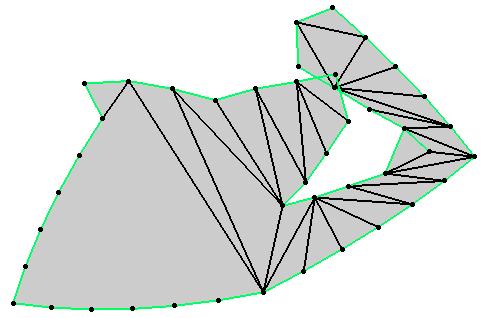
Minimum-perimeter selfoverlapping unfolding (Click
here for ps file).
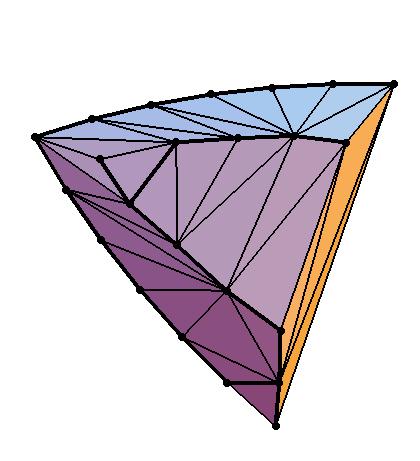
Fig. 3. and its Polytope by Rote (Click
here for ps file).
The smallest among them has 7 facets and 9 vertices, see [Rot97a].
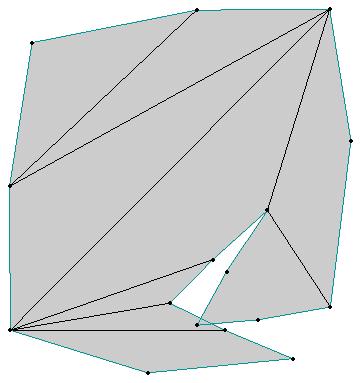
Another minimum-perimeter selfoverlapping unfolding (Click
here for ps file).
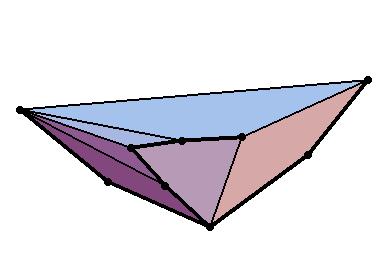
Fig. 3'. and its Polytope by Rote (Click
here for ps file).
Rote constructed also a polytope which admits a combinatorially ambiguous unfolding[Rot97b]. One can construct two combinatorially different polytopes from such an unfolding:
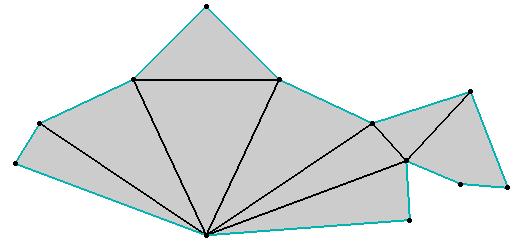
Combinatorially ambiguous unfolding (Click
here for ps file).
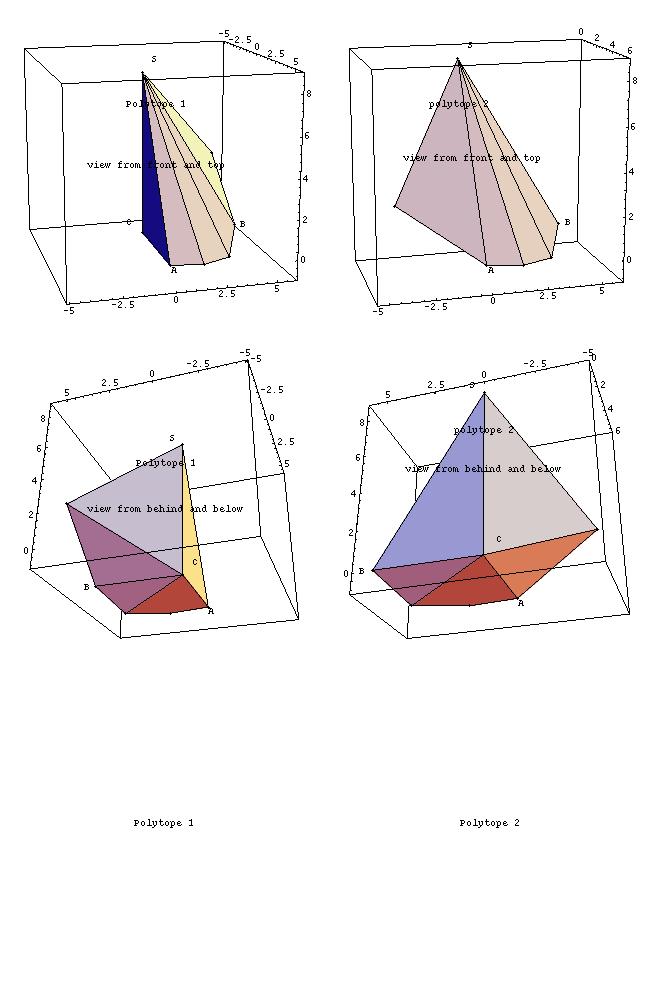
Fig. 4. and its two polytopes by Rote (Click
here for ps file).
Matsui's example mentioned above gives rise to two geometrically different polytopes which are combinatorially equivalent.
Note that a question (related to (a')) on the existence of an unfolding without overlaps, where it is allowed to cut any place in the boundary, was answered positively by Aronov and O'Rouke [AO91]. The key idea was to cut through geodesic paths from a fixed vertex to all other vertices. In fact this result motivates us to pose another open problem.
Recently, Mr. Wolfram Schlickenrieder (schlicke@math.tu-berlin.de) has reported that he found several examples that answered the question above negatively. We shall post some example(s) as soon as we verify his claim.
This page is created by Komei Fukuda with help of latex2html